什么是图？

图是一种数据结构，它能很容易的建模现实场景中的一组实体之间的复杂关系。在现实世界中，很多数据往往会以图的形式出现，例如社交网络、电商购物等。因此，近些年来使用智能化方式来建模分析图结构的研究越来越受到关注, 其中基于深度学习的图建模方法的图神经网络(Graph Neural Network, GNN), 因其出色的性能已广泛应用于社会科学、自然科学等多个领域。

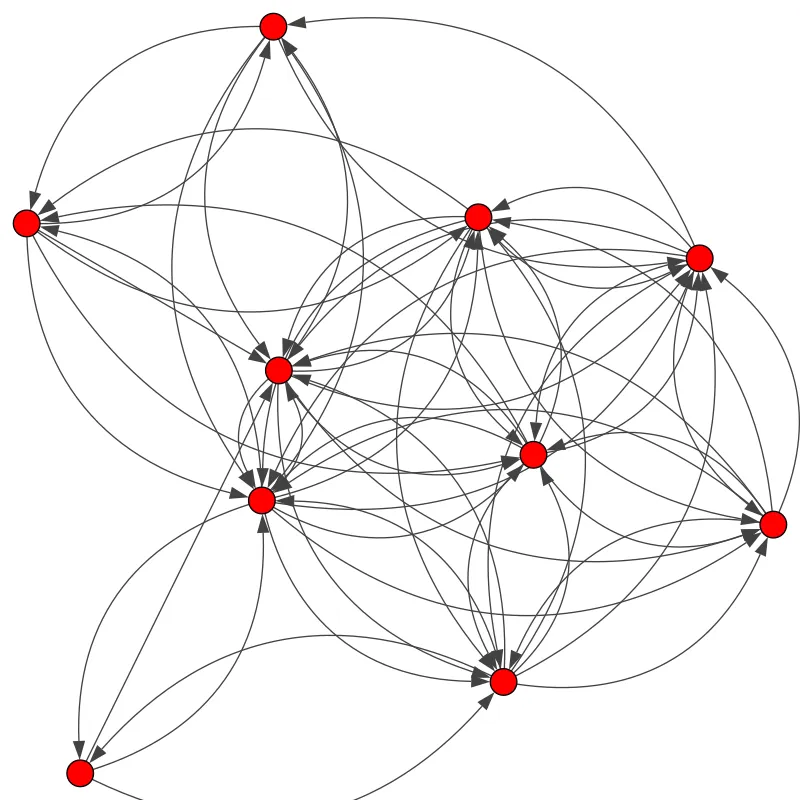
有向图的学习笔记1 动态更新 - 知乎

边上面的黑色尖头表示节点之间的关系类型，其可表明一个关系是双向的还是单向的。图有两种主要类型：有向图和无向图。在有向图中，节点之间的连接存在方向；而无向图的连接顺序并不重要。有向图既可以是单向的，也可以是双向的。

图可以表示很多事物——社交网络、分子等等。节点可以表示用户/产品/原子，而边表示它们之间的连接，比如关注/通常与相连接的产品同时购买/键。社交网络图可能看起来像是这样，其中节点是用户，边则是连接：

社交网络PNG图片素材下载_图片编号qxjdamlv-免抠素材网

节点表示用户，边则表示两个实体之间的连接/关系。真实的社交网络图往往更加庞大和复杂！

图的基本概念

通常使用 $G = ( V , E )$ 来表示图，其中 $V$ 表示节点的集合、 $E$ 表示边的集合。对于两个相邻节点 $u , v$ 使用 $e = ( u , v )$ 表示这两个节点之间的边。两个节点之间边既可能是有向，也可能无向。若有向，则称之有向图(Directed Graph), 反之，称之为无向图(Undirected Graph)。

图的表示

在图神经网络中，常见的表示方法有邻接矩阵、度矩阵、拉普拉斯矩阵等。

邻接矩阵(Adjacency Matrix)

用于表示图中节点之间的关系，对于n个节点的简单图，有邻接矩阵 $A∈R^{n×n}$ :

A_{ij} = \begin{cases} 1 & if(v_i,v_j)∈E & and& i≠j \\ 0 & else \end{cases}

度矩阵(Degree Matrix)

节点的度表示与该节点相连的边的个数，记作 $d(v)$ 。对于n个节点的简单图 $G = ( V , E )$ ，其度矩阵D为 $D_{ii}=d(v)$ ，也是一个对角矩阵。

拉普拉斯矩阵(Laplacian Matrix)

对于n个节点的简单图 $G = ( V , E )$ ，其拉普拉斯矩阵定义为 $L=D-A$ ，其中D、A为上面提到过的度矩阵和邻接矩阵. 将其归一化后有 $L^{sym}=D^{-1/2}LD^{-1/2}$ 。

图神经网络的基本概念

了解图神经网络

每个节点都有一组定义它的特征。在社交网络图的案例中，这些特征可以是年龄、性别、居住国家、政治倾向等。每条边连接的节点都可能具有相似的特征。这体现了这些节点之间的某种相关性或关系。

假设我们有一个图 G，其具有以下顶点和边：

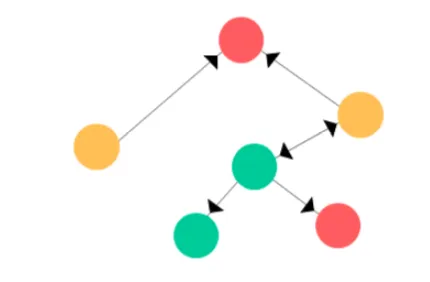
为了简单起见，假设图节点的特征向量是当前节点的索引的one-hot编码。类似地，其标签（或类别）可设为节点的颜色（绿、红、黄）。那么这个图看起来会是这样：

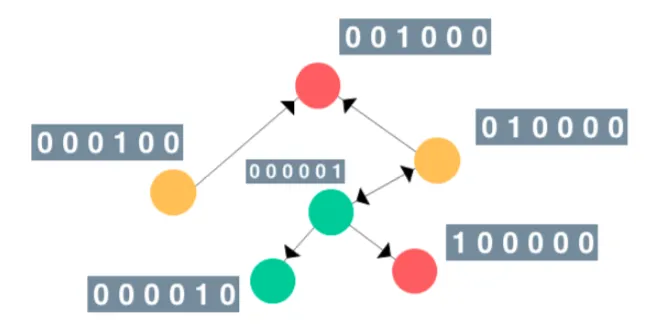
节点的顺序并不重要。

注意：在实际运用中，尽量不要使用 one-hot 编码，因为节点的顺序可能会非常混乱。相反，应该使用可明显区分节点的特征，比如对社交网络而言，可选择年龄、性别、政治倾向等特征；对分子研究而言可选择可量化的化学性质。

现在，我们有节点的 one-hot 编码（或嵌入）了，接下来我们将神经网络引入这一混合信息中来实现对图的修改。所有的节点都可转化为循环单元（或其它任何神经网络架构，只是我这里使用的是循环单元）；所有的边都包含简单的前馈神经网络。那么看起来会是这样：

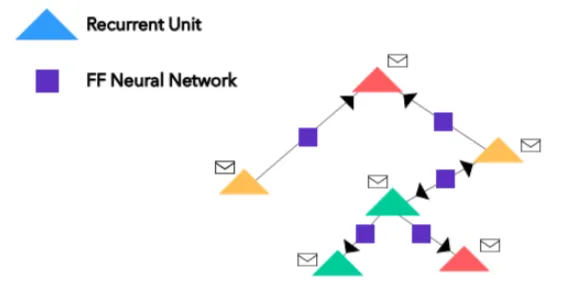
其中的信封符号只是每个节点的 one-hot 编码的向量（嵌入）。

消息传递

一旦节点和边的转化完成，图就可在节点之间执行消息传递。这个过程也被称为近邻聚合（Neighborhood Aggregation），因为其涉及到围绕给定节点，通过有向边从周围节点推送消息（即嵌入）。

注意：有时候可为不同类型的边使用不同的神经网络，比如为单向边使用一种神经网络，为双向边使用另一种神经网络。这样仍然可以获取节点之间的空间关系。

就 GNN 而言，对于单个参考节点，近邻节点会通过边神经网络向参考节点上的循环单元传递它们的消息（嵌入）。参考循环单位的新嵌入更新，基于在循环嵌入和近邻节点嵌入的边神经网络输出的和上使用循环函数。我们把上面的红色节点放大看看，并对这一过程进行可视化：

经典的图神经网络模型

GCN(Graph Convolution Networks)

GCN可谓是图神经网络的“开山之作”，它首次将图像处理中的卷积操作简单的用到图结构数据处理中来，并且给出了具体的推导，这里面涉及到复杂的谱图理论。2017年，Thomas N. Kipf等人提出GCN模型. 其结构如图2所示：

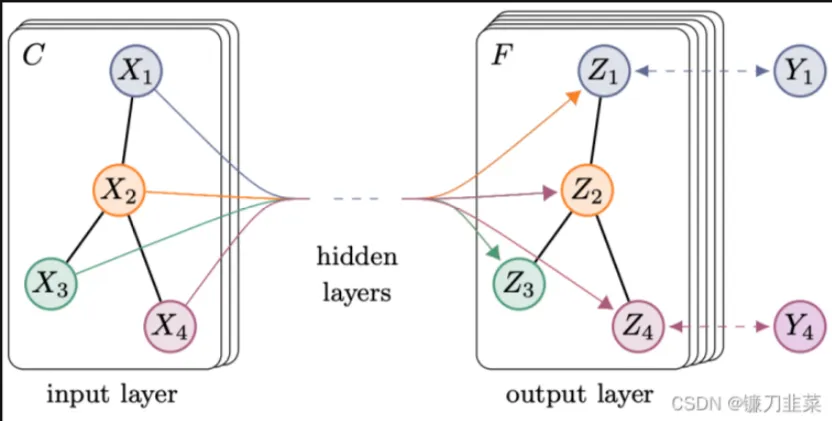
假设需要构造一个两层的GCN，激活函数分别采用 $ReLU和Softmax$ ，则整体的正向传播的公式如下所示：

Z = f(X, A) = \text{softmax}(\hat{A} \text{ReLU}(\hat{A} X W^{(0)}) W^{(1)}) \\ \hat{A} = \hat{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}

其中 $W^{(0)}$ 表示第一层的权重矩阵， $W^{(1)}$ 表示第二层的权重矩阵，X为节点特征， $\tilde{A}$ 等于邻接矩阵A和单位矩阵相加， $\tilde{D}$ 为A的度矩阵。

从上面的正向传播公式和示意图来看，GCN好像跟基础GNN没什么区别。接下里给出GCN的传递公式：

H^{(l+1)} = \sigma (\tilde{D}^{-\frac{1}{2}}\tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)})

观察一下归一化的矩阵与特征向量矩阵的乘积：

\\ \begin{pmatrix} \tilde{D}^{-1} \tilde{A} H \end{pmatrix}_i = \begin{pmatrix} \tilde{D}^{-1} \tilde{A} \end{pmatrix}_i H \\ = \begin{pmatrix} \sum_{k} \tilde{D}_{ik}^{-1} \tilde{A}_i \\ \end{pmatrix}_i H \\ = \begin{pmatrix} \tilde{D}_{ii}^{-1} \tilde{A}_i \\ \end{pmatrix}_i H \\ = \tilde{D}_{ii}^{-1} \sum_j \tilde{A}_{ij} H_j \\ = \sum_j \frac{1}{\tilde{D}_{ii}} \tilde{A}_{ij} H_j

这种聚合方式实际上就是在对邻接求和取平均。而 $\tilde{D}^{-1/2}\tilde{A}\tilde{D}^{-1/2}$ 这种归一化方式，将不再单单地对领域节特征点取平均，它不仅考虑了节点i的度，也考虑了邻接节点j的度，当邻居节点 j度数较大时，它在聚合时贡献地会更少。这也比较好理解，存在B->A<-C<-[D,E,F] 这么一个图，当使用这种归一化矩阵，在对A这个节点的特征进行更新时，B占的权重会更大，C占的权重会更小。因为B对A产生影响，与A对B产生对影响是一样的（无向图），由于B只有A这个邻居，所以A对B影响很大；同样地，C对A产生影响，与A对C产生对影响是一样的，因为C有很多节点，所以A对C节点对影响没那么大，即C对A节点对影响没那么大。

\begin{align*} \left(\tilde{D}^{-0.5}\,\tilde{A}\tilde{D}^{-0.5}\,H\right)_i &=\left(\tilde{D}^{-0.5}\,\tilde{A}\right)_i\tilde{D}^{-0.5}\,H\\ &=\left(\sum_k\tilde{D}_{ik}^{-0.5}\,\tilde{A}_i\right)\tilde{D}^{-0.5}\,H\\ &=\tilde{D}_{ii}^{-0.5}\,\sum_j\tilde{A}_{ij}\sum_k\tilde{D}_{jk}^{-0.5}\,H_j\\ &=\tilde{D}_{ii}^{-0.5}\,\sum_j\tilde{A}_{ij}\tilde{D}_{jj}^{-0.5}\,H_j\\ &=\sum_j\frac{1}{\sqrt{\tilde{D}_{ii}\,\tilde{D}_{jj}}}\,\tilde{A}_{ij}H_j \end{align*}

通过实验证明GCN性能出色，GCN即使不训练，提取出来的特征已经非常优秀。

GCN在空间上自动聚类从上图可以发现，使用随机初始化的GCN进行特征提取，经过GCN的提取出的embedding，已经在空间上自动聚类了。

GCN的缺点

GCN需要将整个图放到内存和显存，这将非常耗内存和显存，处理不了大图。
GCN在训练时需要知道整个图的结构信息(包括待预测的节点), 这在现实某些任务中也不能实现(比如用今天训练的图模型预测明天的数据，那么明天的节点是拿不到的)。

GAT：Attention机制

为了解决GNN聚合邻居节点的时候没有考虑到不同的邻居节点重要性不同的问题，GAT借鉴了Transformer的idea，引入masked self-attention机制，在计算图中的每个节点的表示的时候，会根据邻居节点特征的不同来为其分配不同的权值。

Thanks for reading!

图神经网络详解

2025年 09月07日 20:42 星期日

2128 字 · 8 分钟

图神经网络 GNN GCN Kaku