本文作者先是分析了图修改攻击(graph modification attack, GMA)和图注入攻击(graph injection attack, GIA)的区别以及图注入攻击相比图修改攻击的优势。然后作者又基于KDD-CUP 2020中的GIA任务在黑盒攻击和规避攻击的条件下引出了自己的攻击方法拓扑缺陷图注入攻击(Topological Defective Graph Injection Attack)

黑盒攻击：描述了攻击者对模型的了解程度，再黑盒条件下，攻击者可以像用户一样与模型进行交互，但无法知晓其内部细节，攻击者不知道目标模型的内部结构、参数、训练数据等细节。他只能通过向模型提供输入并观察其输出（如预测标签、置信度分数）来获取有限的信息。

规避攻击： 描述了攻击发生的时间节点，主要发生在模型训练部署之后的推理阶段， 攻击者不改变模型本身，而是在输入数据上精心构造细微的、人眼难以察觉的扰动，使得训练好的模型在处理这个被“污染”的输入时做出错误的判断。

TDGIA

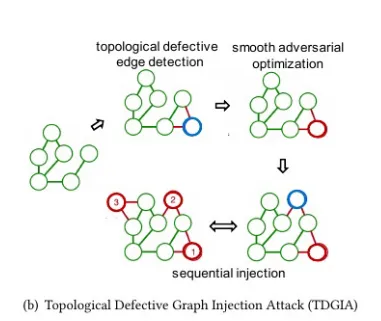
TDGIA分为拓扑缺陷边选择和平滑对抗优化两个模块，gnn作为非结构无关模型，很容易通过注入节点改变其结构完成注入攻击。

优势

TDGIA不同于NIPA以及AFGSM是在投毒模式下进行攻击的，TDGIA则使用规避攻击，这样就不再需要对每次攻击的防御模型进行重新训练，只需将注入训练完成的整个图数据输入到防御模型中即可。另外TDGIA可以处理NIPA无法处理的大规模图。TDGIA使用了一种更通用的方式来实现对图拓扑结构的修改，从而适用更多的gnn模型。并且该方法同样适用于KDD-CIP 2020中的顶级防御方案。

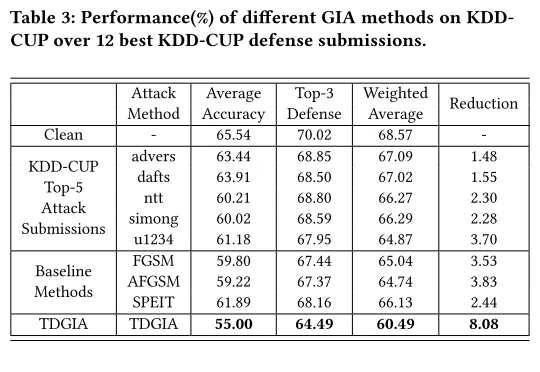
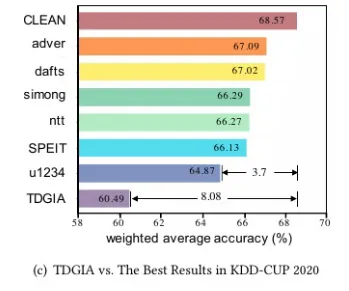
下图是不同攻击方法的比较。

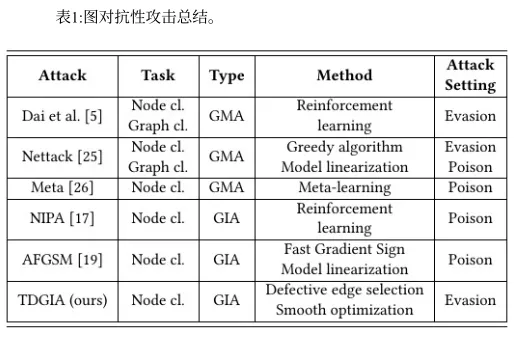
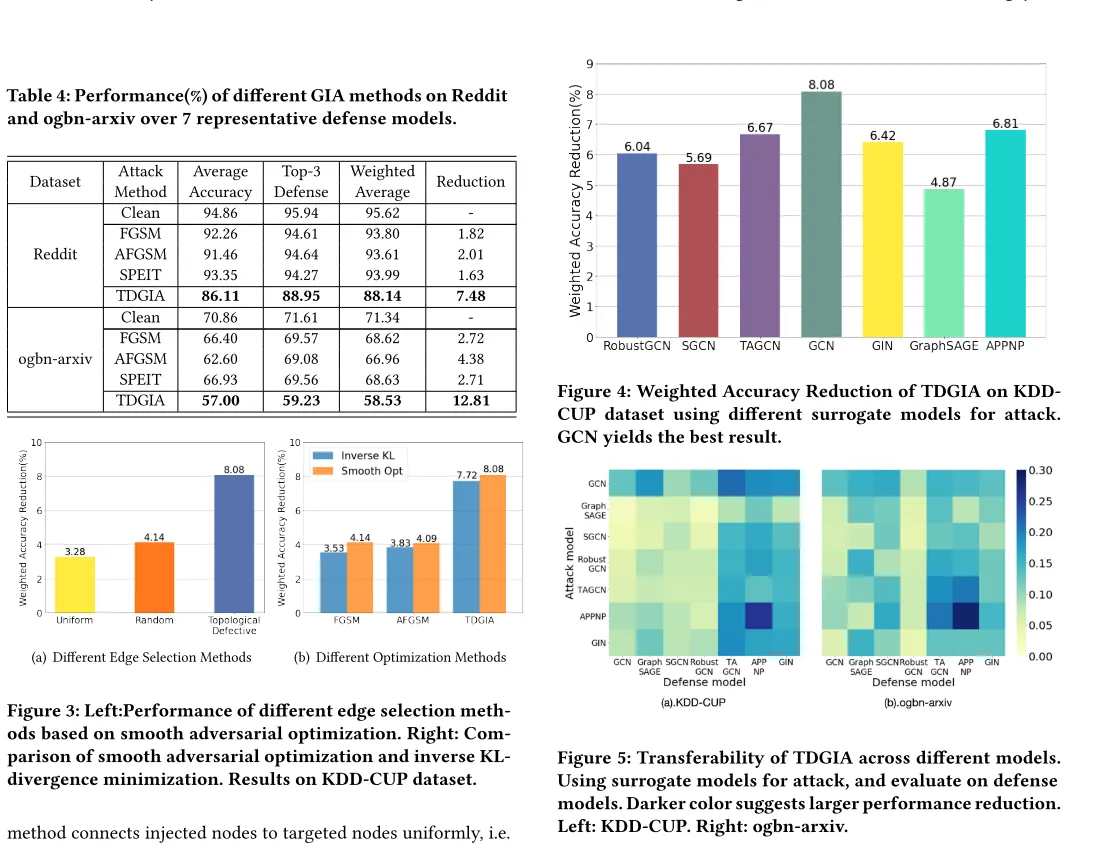
下图列出了TDGIA相比其他攻击方案对防御模型攻击后的准确度情况。

拓扑缺陷边选择

首先通过某种方法寻找合适的注入点，并将节点和原有节点连接，如下图所示。

A为原图的邻接矩阵,$A_I$是注入节点之间的邻接矩阵，$V_I$是原始节点与注入节点之间的边的矩阵。N为原始节点数量,$N_I$为注入节点数量,D为特征个数,F是原始节点的特征矩阵,$F_I$是注入节点的特征矩阵。

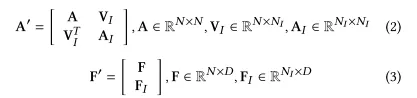
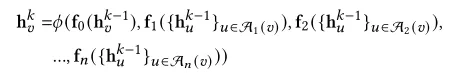
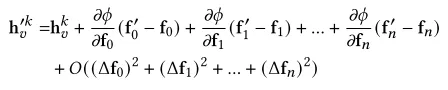
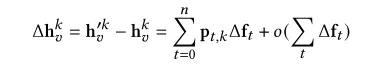
下图中$f_t$表示gnn中聚合函数的变化值.加号前半部分表示所有原节点权重变化值(因为注入了新节点,导致原节点的权重发生变化)和上一层对应特征向量的矩阵乘积,加号后半部分表示所有注入节点权重值和其上一层对应特征向量的矩阵乘法。

y便是节点,t表示第几跳(中心节点v到某节点经过的边数)

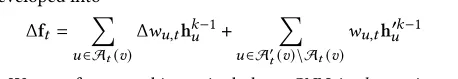
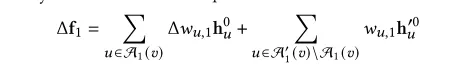
注入节点权重值的选取,在GCN模型下已经以GCN为基础的模型我们使用度对称归一化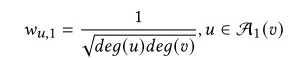

在基于平均池化层的GNN(例如GraphSAGE中)使用

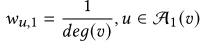
而TDGIA中我们决定注入点链接哪些节点,我们使用上述两个式子的组合形式来得出拓扑脆弱性:

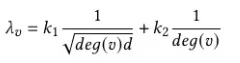
deg(v)表示v节点的度,d表示注入节点的度(即链接几个节点),k1,k2为超参数,用于平衡两种不同GNN架构的影响。

低度数节点（deg(v)小）的 λ_v值更大，更容易被攻击。这与直觉一致：在一个社交网络中，一个朋友很少的人（低度数节点）比一个名人（高度数节点）更容易受到一个新朋友（注入节点）的影响。

平滑对抗性

这一步的目标是在已经确定注入节点连接方式（拓扑缺陷边）的基础上，为这些注入节点生成有效的特征，以完成攻击。在完成边选择后，注入节点的特征最初是零（或随机值）。这一步的目标是优化这些特征，使得模型对目标节点的预测错误。同时，要确保优化过程稳定，并且生成的特征不易被防御机制检测为异常。

优化注入节点的特征,使图中原节点的预测效果变差,通常使用与模型训练相反的损失函数,负KL散度$L_v = −𝐷_{𝐾𝐿}(Y_{true}||Y_{pred}) = ln(𝑝_{𝑦_{𝑣,Pred}}=𝑝_{𝑦_{𝑣,true}}) = ln𝑝_v$是模型将节点正确分类的概率

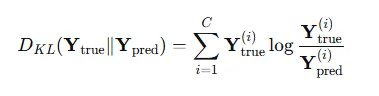
这里 CC 是类别的总数。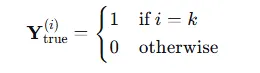

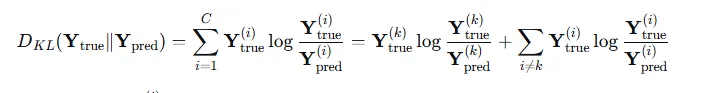
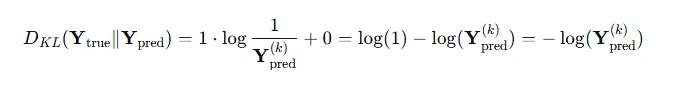
通常，机器学习中默认使用自然对数ln,而$Y_{pred}$ 就是模型预测的正确类别的概率，也就是公式中的 $p_v$

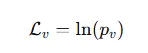
但上面这种损失函数存在梯度爆炸的风险,其梯度为$1/p_v$。当$p_v$趋近于0的时候,梯度会趋向于+∞,导致优化过程极其不稳定。

所以作者使用更平滑的损失函数,其中r为控制因子,是个正数,他是个阈值,决定了损失函数何时开始生效,类似于激活函数ReLU。

如果 $r > -lnp_v$（即模型仍然有较高的信心正确分类)，则 (r + ln p_v) 为正，取$r+lnp_v$，此时梯度会继续优化,进一步降低$p_v$值。

如果$r <= -lnp_v$，则 (r + ln p_v) 为非正，取0，此时损失为0, 梯度也为0。攻击不再起作用。

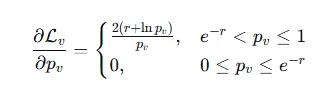
最终目标是最小话所有目标节点的平均平滑损失:

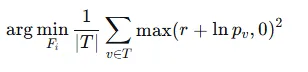
特征值约束

生成的对抗特征不能随心所欲，必须防止被异常值检测器过滤掉。简单方法Clamp方法,在每次优化更新后，强行将特征值限制在 [min, max] 的合理范围内。但该方法如果一个特征值被卡在边界上,会导致该特征无法被优化,可能使攻击效果变差。

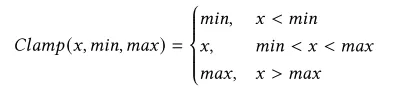
因此使用更平滑的映射函数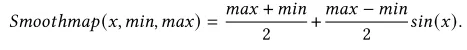,优化流程实际上是优化中间变量x,而不是直接优化最终特征值,通过周期函数sin函数可以将任何值平滑的周期的映射到[-1,1],整个映射函数映射到[min,max]之间。

整个过程

该算法的目的是：通过向原始图中分批注入恶意节点和边，并优化这些节点的特征，生成一个被攻击后的图 G'，使得 代理模型M 在 G' 上对目标节点集 T 的预测准确率下降。

• 输入 (Input):

  • G = (A, F): 原始图（邻接矩阵 A 和节点特征矩阵 F）。
  • M: 代理模型（一个在本地训练的GNN，用于模拟黑盒目标模型）。
  • T: 目标节点集合（攻击者希望使其被误分类的节点列表）。

• 输出 (Output):

  • G' = (A', F'): 攻击后生成的毒化图。

• 参数 (Parameter):

  • b: 注入节点的总数量预算。
  • d: 每个注入节点可以连接的边数预算（度数预算）。
  • Δ_F: 注入节点特征值的约束范围（例如 [0, 1]）。

  第一行: 初始化

  • G' <- G: 将毒化图 G' 初始化为原始图 G。
  • V_I <- 0^{N x N_I}: 初始化一个全零矩阵 V_I，用来表示原始节点与注入节点之间的连接关系。其尺寸为 (原始节点数 N) x (注入节点数 N_I)。
  • A_I <- 0^{N_I x N_I}: 初始化一个全零矩阵 A_I，表示注入节点之间的连接关系（通常注入节点之间不连接）。
  • F_I <- N(0, σ)^{N_I x D}: 初始化注入节点的特征矩阵 F_I。通常用均值为0、方差为 σ 的正态分布随机初始化。其尺寸为 (注入节点数 N_I) x (特征维度 D)。

  第二行: 开始顺序攻击循环

  • 这是一个 while 循环，只要剩余的注入预算 b 大于0就继续执行。
  • 这实现了顺序攻击：分批注入节点，而不是一次性全部注入。

  第3-7行: 计算缺陷分数

  • 对于每个目标节点 v，计算一个最终的缺陷分数 μ_v，用于排名哪些节点最容易攻击。
  • p_v: 使用当前的毒化图 G' 在代理模型 M 上计算节点 v 被正确分类的概率。
  • λ_v: 计算拓扑缺陷因子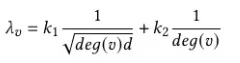 。它衡量节点 v 因度数低而固有的脆弱性。
  • μ_v: 计算最终的缺陷分数。它是 p_v 和 λ_v 的加权组合。
    • α 是一个超参数，用于平衡两部分的影响。
    • (α p_v + (1 - α)) 这部分确保：当前模型越容易正确分类的节点（p_v 大），其得分 μ_v 也越高。这是因为攻击一个目前还很“自信”的节点，潜力更大。
    • 最终，μ_v 分数高的节点是那些既拓扑脆弱（低度数）又尚未被成功攻击（高 p_v） 的节点。

  第8-9行: 选择连接目标并建立缺陷边

  • b_seq: 设定本批次要注入的节点数量（b_seq ≤ b）。
  • Connect 操作: 这是算法的核心动作。
    • 从目标节点集 T 中选出缺陷分数 μ_v 最高的 b_seq * d 个节点。
    • 创建 b_seq 个新节点。
    • 将每个新节点连接到 d 个选出的目标节点上（因为每个注入节点有 d 条边的预算）。
    • 这个连接关系被记录到矩阵 V_I 中。

  第10-11行: 平滑优化注入节点特征

  • 在连接关系固定后，开始优化本批次注入节点的特征 F_I。
  • 优化目标：平滑损失函数 arg min_FI (1/|T| Σ max(r + ln p_v, 0)²)。
  • 优化约束：使用 Clamp 或更先进的 Smoothmap 函数，确保优化后的特征值落在合理范围 Δ_F（如 [0,1]）内，避免被异常检测发现。

  第12-14行: 更新图和预算

  • b <- b - b_seq: 扣除本批次使用的注入节点数。
  • Update A' and F': 将本批次注入的节点和边正式加入到毒化图 G' 中。
    • 邻接矩阵 A' 会变大，加入 V_I 和 A_I 所表示的连接关系。
    • 特征矩阵 F' 也会变大，加入新优化好的特征 F_I。

  第15-16行: 循环结束并返回结果

  • 循环结束，意味着所有的注入预算 b 都已用完。
  • 返回最终生成的、包含所有注入节点和优化特征的毒化图 G'。这个图将被用来攻击黑盒目标模型。

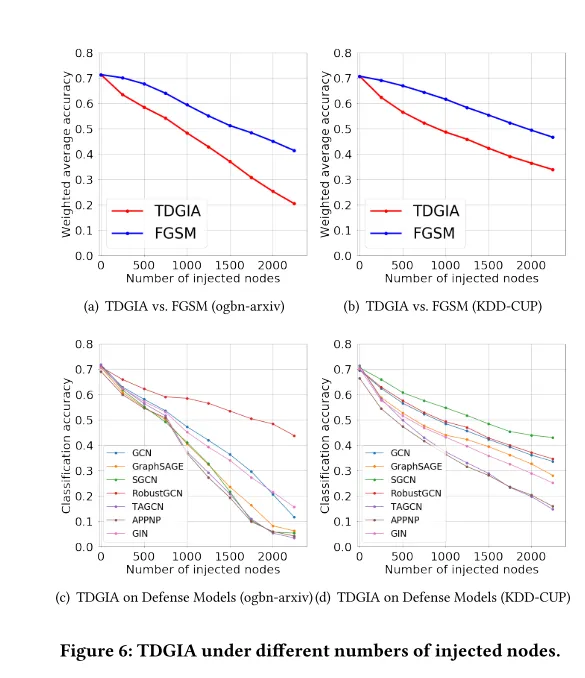
攻击结果